流体表現は、クリエイティブコーディングの作例として人気があります。水のように滑らかに動く描画が気持ちよかったり、マウス操作でインタラクティブに模様が変化する面白さがあります。しかし、いざ自分で作ってみようとすると、情報が学術的すぎたり、サンプルのセットアップが複雑で動かすまでが大変だったりとなかなか難しいものです。オリジナルの表現を追加しにくくて作成を断念した人もいるのではないでしょうか。
そこで本記事では、「誰でもコピペで使える実装」をコンセプトに、Three.jsを使って2D流体を簡潔に再現できるコードと仕組みを解説します。Three.jsについて詳しくなくても、すぐに動かせる構成を目指しました。
2D流体表現のデモ
流体シミュレーションの計算結果として、画面上の各位置における流体の速度(向きと大きさ)が得られます。得られた速度を使って流体の見た目をレンダリングする4種類のデモを用意しました。各デモはマウスドラッグ・タッチ操作で流体を動かせます。
デモ1 流体と背景の合成
流体の速度を使ってマウスドラッグ時に与えた粒子を移動させています。背景と合成する際に、流体の境界を強く歪ませることで光が屈折したような表現ができます。
デモ2 速度の可視化
流体の速度自体を色で可視化したデモです。水が流れて広がるるような模様が流体の動きに合わせて変化します。
もっとも基本的なデモなので、作成する場合はまずはこちらを参考にすると良いでしょう。デモをアレンジする際にはデモのリポジトリーにポイントをまとめています。

デモ3 速度に合わせて画像ワープ
流体の速度を使い、背景画像をワープ(変形)させるデモです。波紋の表現も加えているので、爽やかな印象を与えます。

デモ4 ピクセルの移動
流体の速度を使い、背景画像のピクセルを移動させるデモです。絵の具を混ぜるような表現が可能です。

本デモは、Vite + TypeScriptにThree.jsを組み込んだ環境で作成しています。Viteによる環境構築について、詳しくは記事『jQueryからTypeScript・Reactまで! Viteで始めるモダンで高速な開発環境構築』を参考ください。
描画ライブラリとしてThree.jsを利用していますが、流体計算の実装はThree.jsの機能にはないため、シェーダーを自分で記述できるNodeMaterialクラスを使用します。
シェーダーはTSL(Three.js Shading Language)で記述しているため、シェーダー言語を知らなくてもJavaScript/TypeScriptのみでデモのコードのアレンジが可能です。TSLについて、詳しくは記事『WebGPU対応のThree.jsのはじめ方』を参考ください。また、Three.jsの機能により、WebGPUを使用できない環境ではWebGLでも動作するようになっています。
実装方法の概要
シミュレーションをThree.jsでどう実現しているか、要点を説明します。
粒子法と格子法
流体シミュレーションには大きく分けて粒子法と格子法という2つの手法があります。
- 粒子法:水などの流体を無数の粒子に分けて計算する方式です。粒子同士の距離や相互作用から流れを再現します。粒子ベースなのでスプラッシュや飛沫表現に向いていますが、GPUで実装する場合は粒子間計算が重くなりがちです。
- 格子法:空間を格子状に分割し、各セルに「速度」「圧力」などの値を持たせて計算する方式です。煙や水面のような「連続的な流れ」を表現するのに向いており、今回はこちらの手法を採用しています。
テクスチャーベースの計算
今回のシミュレーションでは、「格子のセル」をテクスチャーのピクセルで表現します。たとえば解像度256×256の流体シミュレーションなら、256×256ピクセルのテクスチャーを用意し、その各ピクセルが「格子セル」に相当します。
テクスチャーにおけるピクセルの位置が格子の座標をあらわし、ピクセルのRGBA値に流体の物理量(速度や圧力など)を格納します。つまり格子法による流体シミュレーションは、テクスチャーを使った数値計算と考えると理解しやすいです。
テクスチャーに値を格納する手段として、フラグメントシェーダーを使用します。フラグメントシェーダーはGPUの並列処理を活かして大量のピクセルを高速に処理できます。各ピクセルに対して、「前フレームのセルや隣のセルから値を読み込み、新しい値を計算して書き込む」という処理を並列に実行します。
テクスチャーのPing-Pong
シミュレーションでは「次の状態」を計算するために、前の状態を参照する必要があります。しかし、テクスチャーは「読み込みと書き込みを同時に行えない」制約があります。また、直接テクスチャーを書き換えてしまうと、他のピクセルが前の状態を参照できなくなってしまいます。
そこで用いるのがPing-Pongバッファーです。テクスチャーAを読み込み元にして、フラグメントシェーダーで次の状態を計算し、テクスチャーB(フレームバッファー)に書き込みます。次のフレームではテクスチャーBを読み込み元にして、今度はテクスチャーAに書き込みます。
これを交互に繰り返すことで「古い値を参照しながら新しい値を書き込む」処理が実現できます。このような処理をPing-Pongといい、Three.jsなどでテクスチャーに値を格納する場合によく使います。
テクスチャーに格納する物理量
流体シミュレーションの計算で最終的に欲しいものは格子セルの「速度」です。得られた速度を使って流体の見た目をレンダリングします。また、今回のシミュレーションでは、他にも「圧力」および「発散」の値が計算過程で必要になります。
今回は速度(X方向、Y方向)・圧力・発散4つの値をテクスチャーに格納します。ちょうどテクスチャーにはRGBAの4チャンネルがあるので、1つのテクスチャーに4つの物理量をまとめて格納できます。数値の精度を上げたり、他の物理量を格納したい場合には複数枚のテクスチャーに分けることも可能ですが、1枚のテクスチャーにおさめることでGPUのメモリ効率や保存の速度を向上できます。
まとめ
今回紹介したデモは「水や煙のような動き」をインタラクティブに再現する仕組みをベースにしており、見た目のインパクトが大きく、ウェブサイトの演出やUIのちょっとしたアクセントとしても活用できます。
まずは記事のコードを動かしてみて、サイトの背景などに組み込んでみてください。難しい数式を理解しなくても、コピペと少しの調整で自然な動きが加わり、ウェブサイトの表現を向上できるでしょう。
コラム:シミュレーション手法の概要
シミュレーションの計算について説明します。難しい話も含むので、デモを扱うだけの場合はここを読み飛ばしても構いません。シミュレーションの背後について知りたい場合に参考にしてください。
Stable Fluidsと流体の方程式
今回のデモでは「Stable Fluids」という手法を使っています。Stable Fluidsは下記のような特徴をもち、ウェブ上での流体表現として広く使われています。
- 安定性を重視しており、大きめのタイムステップでも破綻しにくい
- リアルタイムな応答性を保つ
- 視覚的に自然な動きを実現できる
Stable Fluidsは、流体の方程式をリアルタイムの数値シミュレーションで扱いやすいように工夫した手法です。
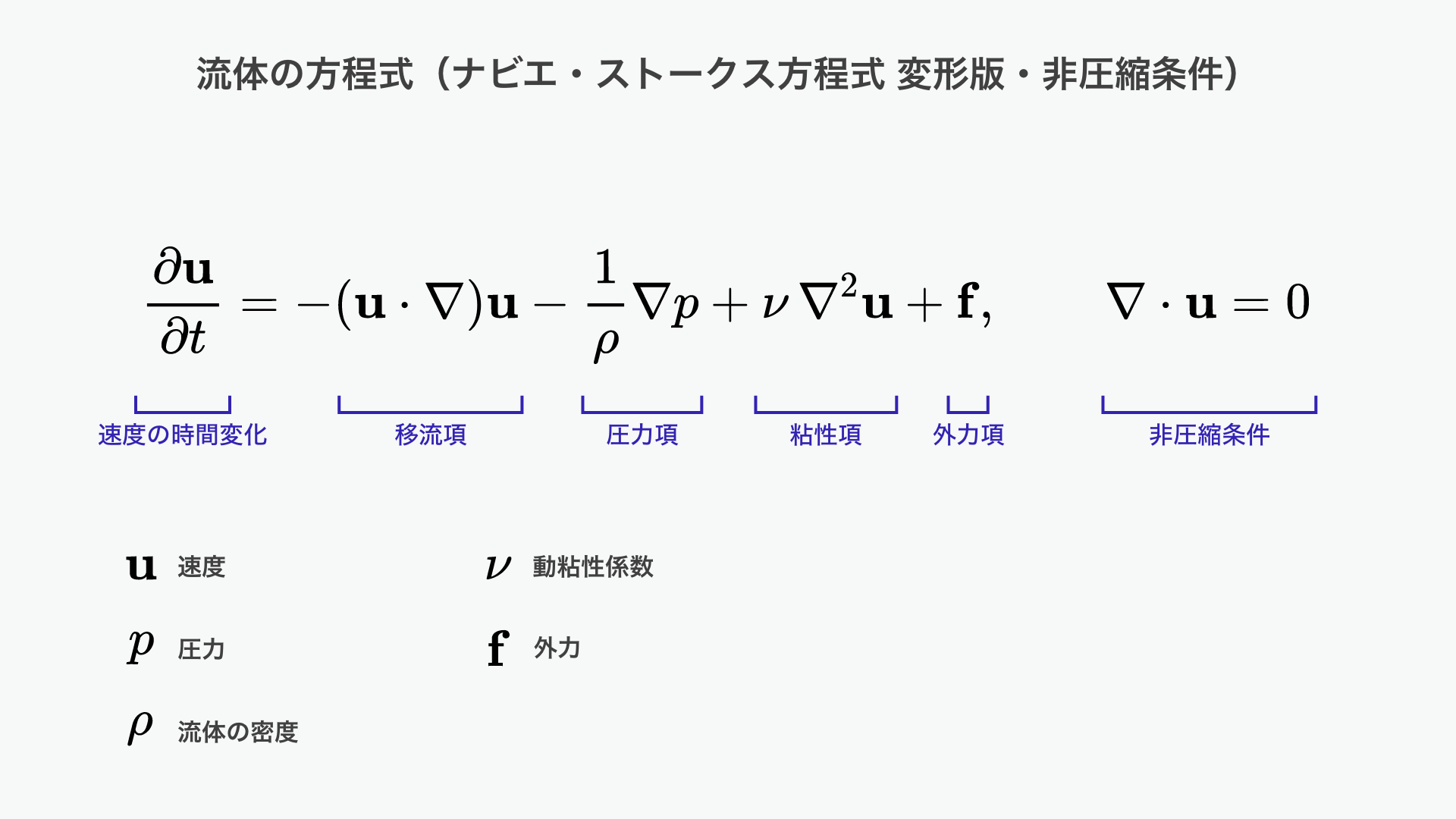
流体の方程式をかんたんに説明すると、「流体の速度が時間とともにどのよう変化するか(左辺)」を、動きを生み出す力(右辺)で表現しています。
流体の方程式だけでは圧力の値が決まらず、速度の整合性も保てません。そこで「流体は湧き出したり消えたりしない」という制約(非圧縮条件)を加えています。これにより圧力が一意に決まり、流体が湧き出さない自然な速度場を計算できるようになります。
方程式の各項は次のようにそれぞれ異なる物理的効果を表しています。
1.移流項
流体が「自分自身の流れ」によって運ばれる効果です。本シミュレーションでは前ステップの速度場を使用して、現在の速度場を補間することで移流を実装しています。
2.圧力項
圧力が高いところから低いところへ押し出される力です。本シミュレーションでは、周囲の圧力とつり合うように修正する計算を反復的に行い、非圧縮条件を満たすように近似的に圧力を逆算しています。
3.粘性項(拡散項)
速度の差をならす摩擦のような効果を計算します。この項がなくても流体として充分自然に見えるため、本シミュレーションでは割愛しています。見かけ上の粘性のような動きは移流項でも表現できるためです。
4.外力項
重力などの外から与えられる力です。実装では、速度場に直接ベクトルを加算することで外力とします。本シミュレーションでは、ユーザーのインタラクションを外力として加えています。
シミューレーションの計算ステップ
流体の方程式は力をあらわす各項が加算された形ですが、実際の数値シミュレーションでは項ごとに処理を分けて順番に適用することで近似的に計算を進めています。
実際の計算ステップは下記のとおりです。それぞれの計算ステップは前ステップの計算結果を使用するため、Three.jsのレンダリング実行(ドローコール)を分ける必要があります。
- 外力の適用:速度場に外力を加算します。
- 移流の計算:現在速度と経過時間から前ステップの速度を参照することで移流を適用します。
- 発散の計算:その時点での速度場の発散を計算します。次の圧力の計算で使用します。
- 圧力の計算:速度と発散から非圧縮条件を満たすように圧力を計算します。
- 速度場の更新:計算された圧力を使って速度場を更新します。
- 描画:更新された速度場を使って流体の見た目をレンダリングします。
今回のデモでも、この順番に沿って計算を実行しています。例として、もっともシンプルなデモ2ではステップの通りに計算を実行しています。また、次のソースコードが各ステップの計算に対応したシェーダーです。

