再帰呼び出しを使おう
関数の中で、自分自身を呼び出すことができます。 これを、再帰呼び出しと呼びます。
myFunc(10);
function myFunc(level){
// 再帰呼び出しのレベルが0より大きかったら
if(level > 0){
console.log(level);
// 再帰レベルを更新
level = level - 1;
// 再帰呼び出しをする
myFunc(level);
}else{
// 再帰呼び出し終了
}
}
グラフィックの分野ではフラクタル図形の描画に役立ちます。
三角形を描こう
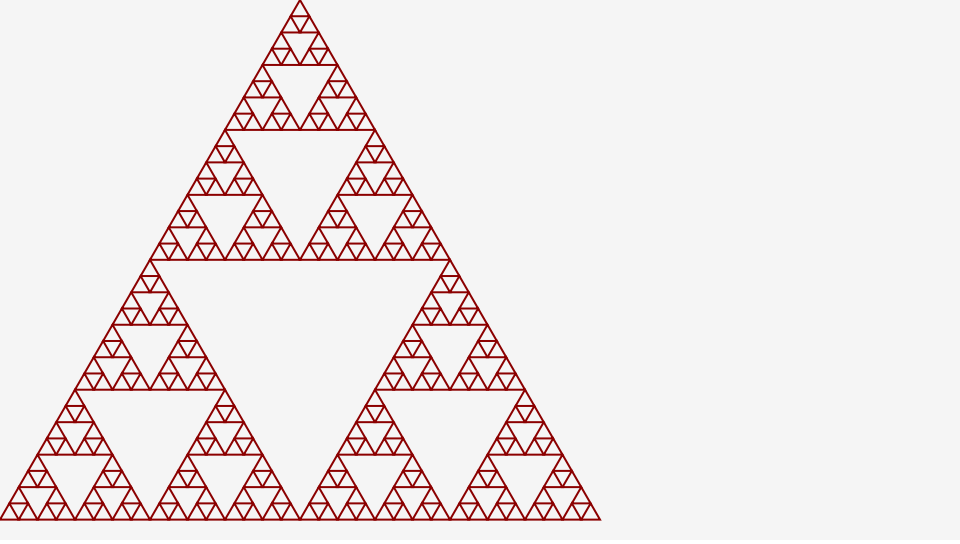
これはシェルピンスキーギャスケットと呼ばれるフラクタル図形の1種であり、無数の三角形からできています。ポーランドの数学者ヴァツワフ・シェルピンスキにちなんで名づけられれました。詳しくはWikipediaで紹介されているので参考にしてください。

再帰呼び出しの構造を確認しましょう。level変数が5から始まり、0になるまで再帰呼び出しによって繰り返し呼びだされます。
// フラクタルの三角形を描く
drawTriangle(5, ・・・);
// 三角形を描く関数
function drawTriangle(level,・・・) {
// 再帰レベルが0になったら描く
if (level <= 0) {
// 再帰終了
// ①
} else { // 再帰レベルが 0 になるまで細分化を行う
// 正三角形の3辺の中点を求める
// ②
// 再帰レベルを更新
level = level - 1;
// 中点を元に細分化を行う
drawTriangle(level, ・・・);
drawTriangle(level, ・・・);
drawTriangle(level, ・・・);
}
}
①の部分では三角形を描きます。lineTo()とmoveTo()メソッドを使って三角形を描きましょう。
// 線の種類を設定
shape.graphics.beginStroke("DarkRed").setStrokeStyle(2.0);
// 三角形を描く
shape.graphics.moveTo(x1, y1); // 始点を設定
shape.graphics.lineTo(x2, y2); // 始点と2点目を結ぶ
shape.graphics.lineTo(x3, y3); // 2点目と3点目を結ぶ
shape.graphics.closePath(); // 始点まで結ぶ
②の部分では細分化のため、三角形の中点を求めます。
// 正三角形の3辺の中点を求める
// 1辺目の中点
var nx1 = (x1 + x2) / 2;
var ny1 = (y1 + y2) / 2;
// 2辺目の中点
var nx2 = (x2 + x3) / 2;
var ny2 = (y2 + y3) / 2;
// 3辺目の中点
var nx3 = (x3 + x1) / 2;
var ny3 = (y3 + y1) / 2;
木を描こう
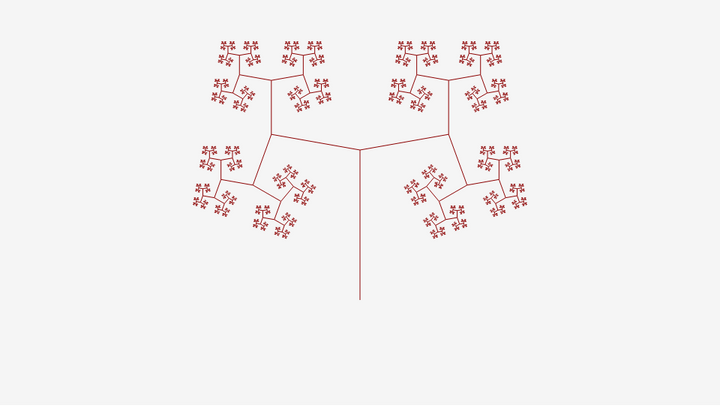
// 枝を描く
function drawTree(x1, // 始点のX座標
y1, // 始点のY座標
leng, // 枝の長さ
angle, // 枝の伸びる方向(角度)
level) // 再帰レベル
{
// 次の枝の座標を算出
var x2 = leng * Math.cos(angle * Math.PI / 180) + x1;
var y2 = leng * Math.sin(angle * Math.PI / 180) + y1;
// 線の種類を設定
shape.graphics.setStrokeStyle(1).beginStroke("DarkRed");
// 枝を結ぶ
shape.graphics.moveTo(x1, y1);
shape.graphics.lineTo(x2, y2);
// 細分化
if (level > 0) {
// 細分化レベルを更新
level = level - 1;
// 次の枝を描く
drawTree(x2, y2, leng * 0.6, angle + 80, level);
drawTree(x2, y2, leng * 0.6, angle - 80, level);
}
}
アニメーションする木を描こう
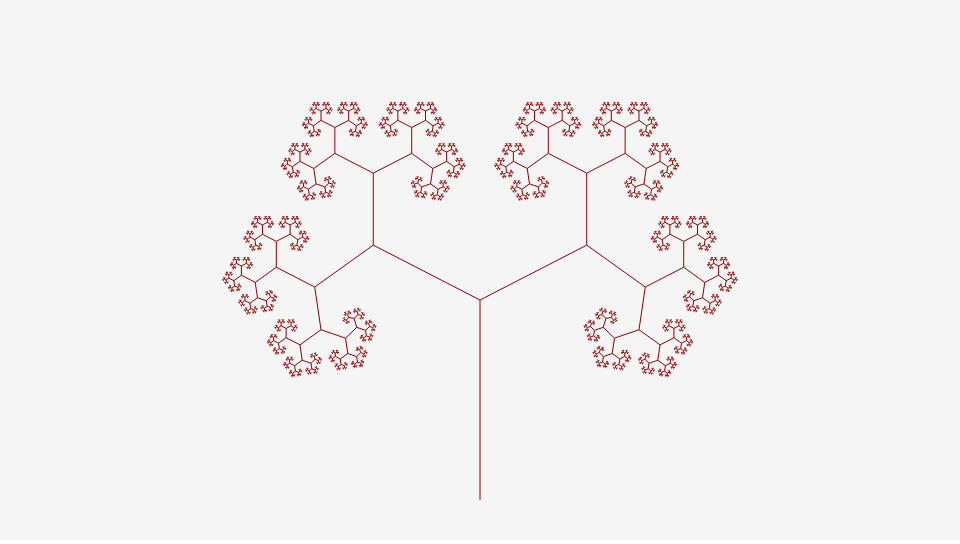
時間経過によって変数timeの値が加算されるようにします。
// 時間経過を変数でカウント
var time = 0;
createjs.Ticker.addEventListener("tick", handleTick);
function handleTick() {
// シェイプをクリアする
shape.graphics.clear();
// フラクタルの木を描く
drawTree(0, 0, 200, 0, 12);
// 画面を更新
stage.update();
// 時間を更新
time += 1;
}
drawTree()関数内部で枝の角度を決定する部分を、time変数依存にします。time変数は時間経過で変化するため、時間経過にしたがって枝の角度が変化します。
// 枝を描く
function drawTree(x1, // 始点のX座標
y1, // 始点のY座標
leng, // 枝の長さ
angle, // 枝の伸びる方向(角度)
level) // 再帰レベル
{
(省略)
// 細分化
if (level > 0) {
// 細分化レベルを更新
level = level - 1;
// 三角関数で変動する値を得る (-1.0〜+1.0の周期になる)
var timeValue = Math.sin(time * Math.PI / 180);
var rot = 40 * ( timeValue + 1.0 ) + 20; // +20〜+100の値を得る
// 次の枝を描く
drawTree(x2, y2, leng * 0.6, angle + rot, level);
drawTree(x2, y2, leng * 0.6, angle - rot, level);
}
}