この記事は前回の「WebGL開発に役立つベクトルの足し算・引き算 (Three.js編)」の続編です。前回まではベクトルの足し算、引き算を勉強しましたが、ベクトルはまだまだ便利な性質を持っています。今回はみなさんが高校で学んでいるはずの内積について紹介します。

内積と聞いて身構えてしまう方もいると思いますが、前回と同様にThree.jsが難しい計算は担ってくれるのでご安心を。一緒に内積についておさらいし、その内積をThree.jsでどう応用していくかを学んでいきましょう。

内積を使った3Dのデモの紹介

本題に入る前に内積を使ったデモを作成したので紹介します。今回は以下のようなライトで照らすような処理を内積を使って実装しています。サンプルコードもGitHubにアップしているので参考ください。

• デモを別ウインドウで再生する
• ソースコードを確認する

※このデモはThree.js(r141)で作成しています。

内積のおさらい

内積とは

内積とはベクトルの掛け算です。内積は「OA・OB」のようにドット繋ぎで表記します。式で表すと以下のようになります。

OA・OB = |OA||OB|cosθ

たとえば、OAベクトルが長さが2、OBベクトルの長さが1、その2つのベクトルのなす角が60度の場合、

OA・OB = |OA||OB|cosθ = 2 x 1 x 0.5;

となり、内積は1となります。この結果からもわかるように内積は計算結果がベクトルではなく数値になります。足し算や引き算の場合は計算結果がベクトルになっていましたが内積は数値になるので覚えておきましょう。

Three.jsでの内積の計算

Three.jsで内積を計算する場合は、THREE.Vector2クラスもしくはTHREE.Vector3クラスに用意されているdot()メソッドを使用します。さきほどの式をJavaScriptで表現すると以下のようになります。

const vOA = new THREE.Vector2(1, Math.sqrt(3));
const vOB = new THREE.Vector2(1, 0);
const value = vOA.dot(vOB); // => 0.5

内積の性質

さきほどの数式を並び替えてみます。

cos0 = OA・OB / |OA||OB|

OAベクトルとOBベクトルが単位ベクトル（長さが1のベクトル）だった場合は

cos0 = OA・OB / 1 x 1 = OA・OB

となります。つまり単位ベクトル同士の内積はcosθを表しています。 この性質は3Dコンテンツを制作する上で非常に役に立ちます。

たとえば、下図のように点CとODベクトルがあるとします。この時、さきほどの性質を使用することで、点CがODベクトルの前後どちら向きにあるかを内積を使って判定できます。

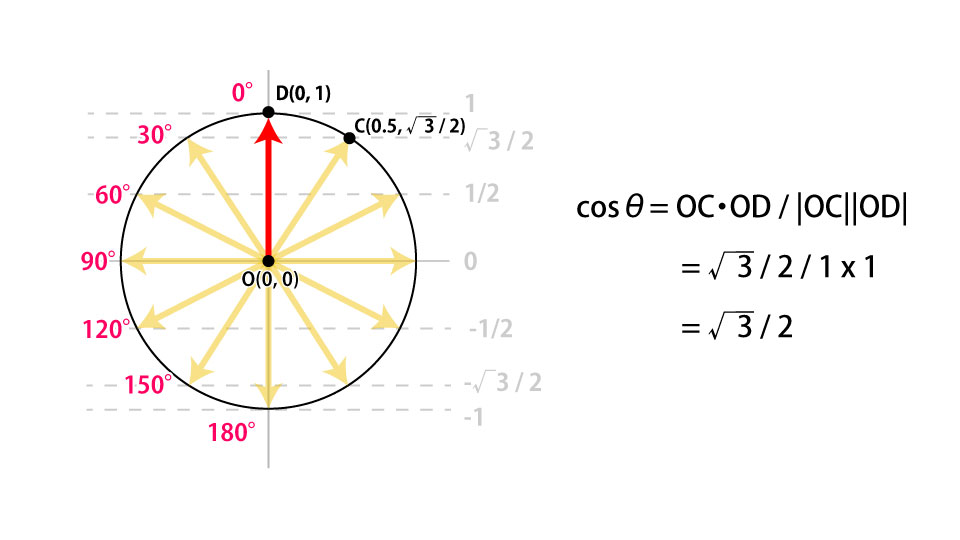
cosθがプラス値であれば前方、マイナス値であれば後方にあると判別できます。上図の場合はcosθが正の値なので前方にあると言えます。今回のデモ作成ではこの性質を活用します。

内積を使ってデモを作成してみよう

冒頭で紹介したデモを実装する為のポイントを解説します。

1. パーティクルをランダムに設置しよう

今回のデモでは球の表面にパーティクルをランダムに設置します。下のコードは1つのパーティクルを生成するための例です。

// スプライト
const particle = new THREE.Sprite(
  new THREE.SpriteMaterial({
    color: 0xffff00,
    opacity: 0.3
  })
);

// ランダムにラジアン角を生成
const phi = ((Math.random() * 180 - 90) * Math.PI) / 180,
  theta = (Math.random() * 360 * Math.PI) / 180;

// 半径を設定
const radius = 50;

// 球の表面にポジションを設定
particle.position.x =
  radius * Math.cos(phi) * Math.cos(theta) * -1;
particle.position.y = radius * Math.sin(phi);
particle.position.z =
  radius * Math.cos(phi) * Math.sin(theta);

同じ処理を必要な数分だけ行い、球の表面にまばらに散るように実装しましょう。球の表面へ設置するための数式に関しては記事「WebGL開発に役立つ重要な三角関数の数式・概念まとめ (Three.js編)」で解説していますので参考ください。

2. 懐中電灯を回転させよう

懐中電灯のメッシュをZ軸を中心に回転させます。下のコードは毎フレーム行う処理の例です。mesh変数には懐中電灯のメッシュが代入されているものとします。

// 現在時間の継続時間に対する進捗度を算出
const progress = (Date.now() - startTime) / 1000;
// 角度を更新
const angle = 150 * progress;
// ラジアン角に変換
const radian = angle * Math.PI / 180;
// ライトを回転
mesh.rotation.z = radian;

コードの通り簡単な処理で回転アニメーションを実現できました。この時、同時にメッシュの正面ベクトル情報も更新しておきます。frontVector変数は事前に宣言されているものとします。

// 正面ベクトルを更新
const x = Math.cos(radian);
const y = Math.sin(radian);
frontVector = new THREE.Vector3(x, y, 0);

さきほど算出したラジアン角をもとに、三角関数を使って懐中電灯の正面ベクトルを求める事ができました。

3. パーティクルの不透明度を設定しよう

懐中電灯の正面ベクトル、パーティクル位置ベクトルの単位ベクトル、2つのベクトルの内積を求め、その値をパーティクルの不透明度として使用します。

// パーティクルの位置ベクトルを複製
const particlePos = particle.position.clone();
// 内積を算出
const dot = particlePos.normalize().dot(frontVector);
// 不透明度に設定
particle.material.opacity = dot;

上記のコードをすべてのパーティクルに実行すると、懐中電灯前方にあるパーティクルのみが表示されます。さらに正面ベクトルと位置ベクトルの方向が近ければ近いほどパーティクルの不透明度が1に近づいていきます。

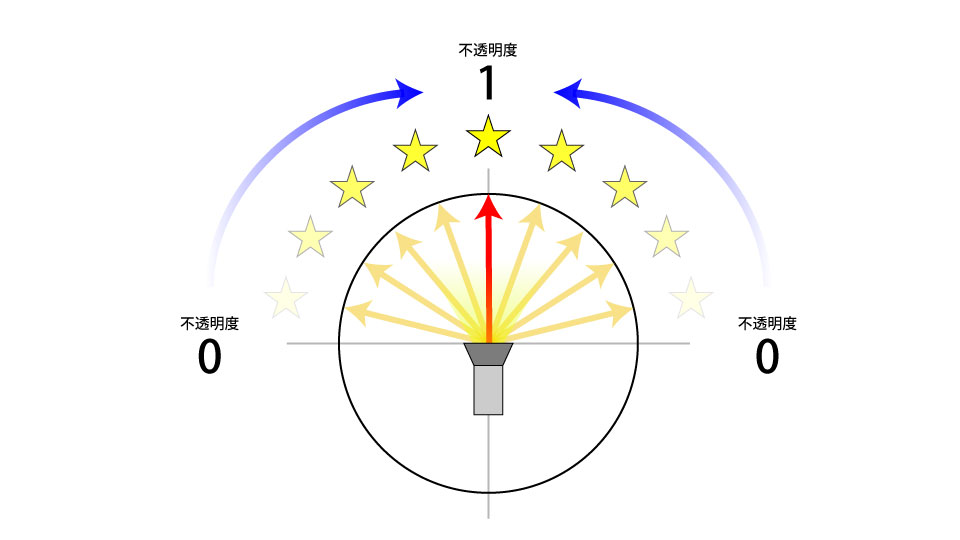
しかし、表示される範囲が広すぎるため少し狭めます。内積が0.8~1.0の場合にのみ表示されるようにしてみましょう。

// パーティクルの位置ベクトルを複製
const particlePos = particle.position.clone();
// 内積を算出
const dot = particlePos.normalize().dot(frontVector);
// 絞り値を設定
const aperture = 0.2;
// 0〜0.2に値を変換
const numerator = dot - (1 - aperture);
// 割合を計算し不透明度に設定
const opacity = numerator / aperture;

これで表示範囲が絞られ、懐中電灯の自然な光になりました。

終わりに

このように内積を使うことで、物体の前後にあるかどうかを判別できることを分かっていただけたと思います。これは3Dキャラクターの視界に敵がいるかどうかの判定や、カメラの視界外の物体は描画しないようにする時などにも応用できます。

今回は2つのベクトルの角度を求める用途で内積を使用しましたが、内積の用途はこれだけではありません。もし興味のある人は内積についてさらに調べてみるとおもしろいと思います。次回は外積について解説しますのでそちらも是非参考ください。