WebGL開発に役立つ重要な三角関数の数式・概念まとめ（Three.js編）

2023年3月15日メンテナンス済み / 株式会社ICS

3Dコンテンツの制作において「三角関数は必須」とよく聞きます。ウェブサイト制作で三角関数を使う場面はほとんどありませんが、WebGLの勉強をすすめると3Dでは三角関数を使う場面が多いことに気づきます。本記事では3Dコンテンツ制作で使用頻度が多い基本的な数式と概念をまとめました。

今回解説する内容は地味ですが、ゲームやデータビジュアライゼーションを作る上でこの数式が基本となってきます。高校数学で学んだことをベースに、3つのサンプルを通して学習できるようまとめましたので、ぜひ最後までお付き合いください。WebGLの人気ライブラリの1つ「Three.js」を使って解説しています。

三角関数を使ったデモの紹介

まずは、本題に入る前に三角関数を使ったデモを作成したので紹介します。次のリンクをクリックしてご覧ください。

Three.jsによる地球の3Dデモ

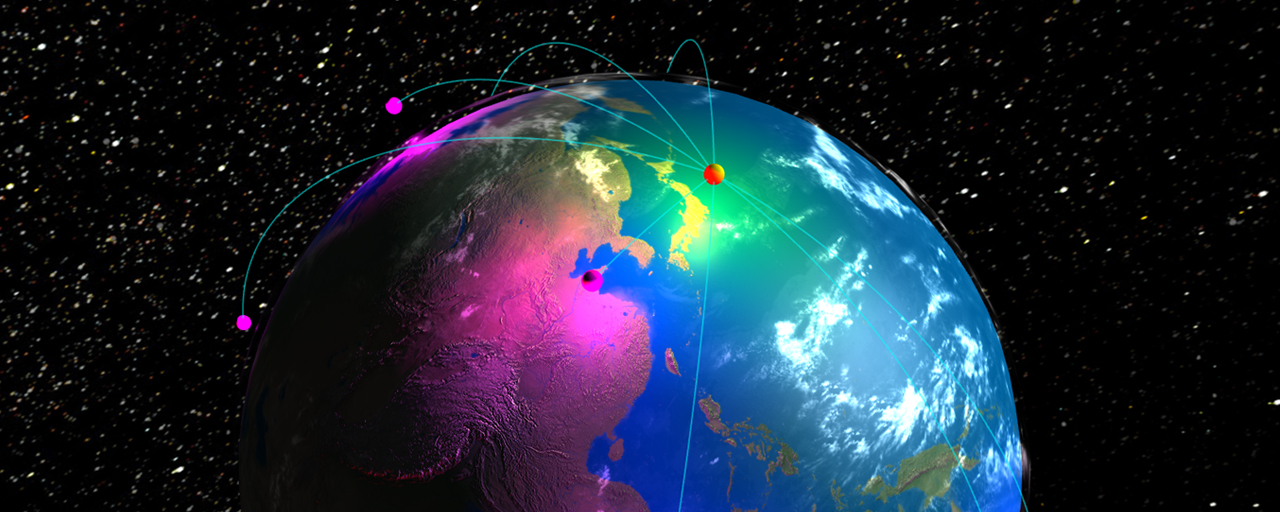
地球をモチーフにしたサンプルです。地球の赤道上には衛星が回り、日本と世界の主要都市は線で結ばれています。本記事の内容を応用することでこのような表現ができるようになります。ソースコードはGitHubに公開していますので、あわせて参照ください。

※この記事のソースコードは2023年3月時点で最新のThree.js(r150)によって書かれています。
※デモで使用しているテクスチャ画像は「Natural Earth III」から引用しています。

1. 円周上を移動する座標の計算方法

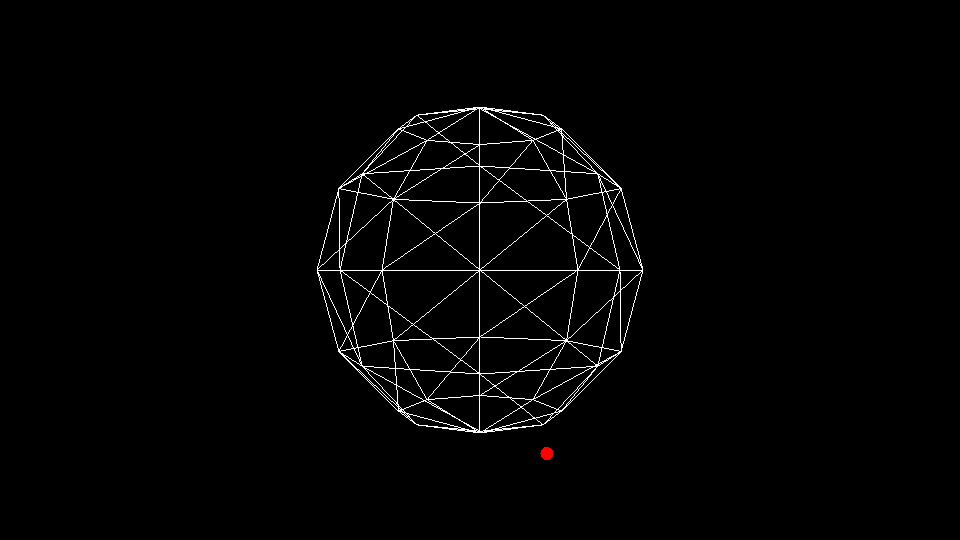
円運動とは1点を中心に円周上を動くモーションのことです。地球の人工衛星や土星の輪っかを想像するとわかりやすいと思いますが、球体の円周上を動く計算式を紹介します。次のサンプルでは、球体のまわりを赤い点が移動します。

下図は円周上にある点のX座標、Y座標を求めるものです。三角関数を使えば角度と半径をもとに公式から座標を求められます。水平の位置を求めるにはコサインを、垂直の位置を求めるにはサインを使います。「サイン・コサイン・タンジェント」と高校のときに暗記しましたが、こんなところで役に立つのですね。

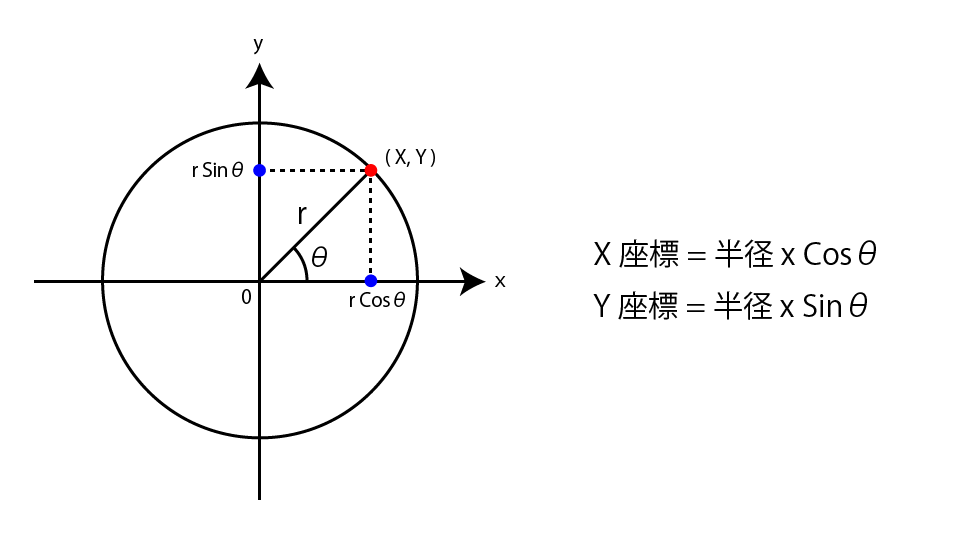
二次元での三角関数

この式を参考に半径と角度を渡して位置情報を返却するコードをJavaScriptで表現してみます。Three.jsでは角度ではなくラジアンを使うので、角度degreeに対してMath.PI / 180を掛け算することでラジアンに変換します。サインとコサインはともにMath.sin()とMath.cos()という命令を使います。

// 角度をラジアンに変換します  
const rad = degree * Math.PI / 180;

// X座標 = 半径 x Cosθ  
const x = radius * Math.cos(rad);  
// Y座標 = 半径 x Sinθ  
const y = radius * Math.sin(rad);

フレーム毎に角度degreeを少しずつ増やすことで、円を描く位置情報を取得できます。

2. 緯度/経度/高度から地球上に点を打つ

世界地図などで地点を示すには緯度と経度がよく利用されますが、緯度と経度を3次元の座標（X・Y・Z）に変換することで都市の場所をプロットできます。次のサンプルでは、地球上の各都市の場所に丸を配置しています。

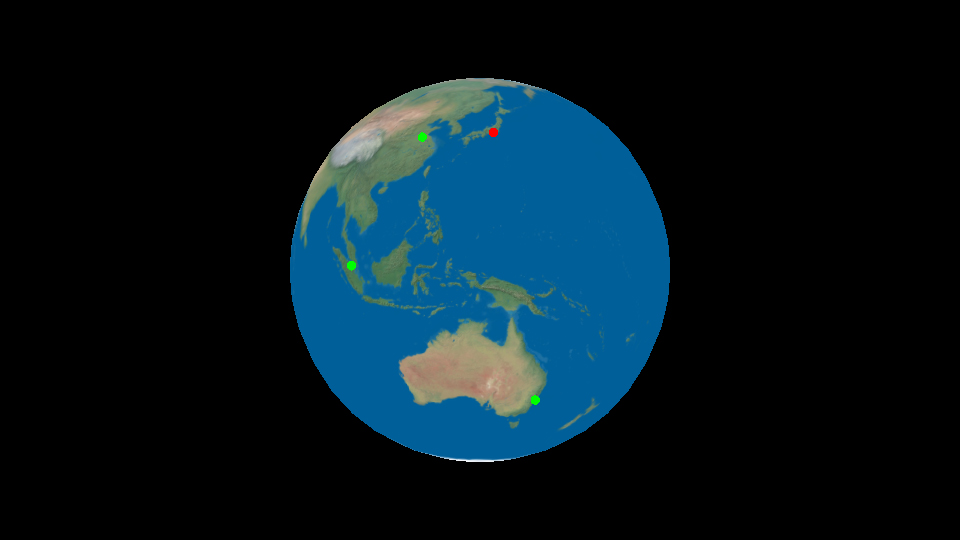
指定した緯度、経度、高度で地球上に点を打てるようにしてみます。前章の円運動では2次元上での位置計算ですが、今回は3次元上での計算になります。下図の式は球上にある点のX座標、Y座標、Z座標を求めるものです。

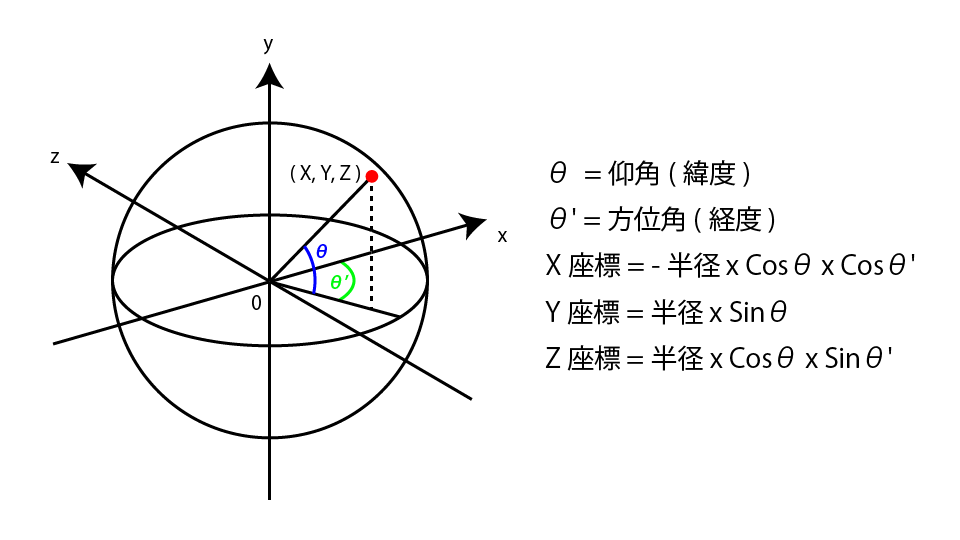
3次元空間による、緯度・経度の座標の算出方法

上の式を参考に緯度、経度、高度を渡して位置情報を返却するJavaScriptの関数を組んでみましょう。

/**
 * 緯度経度から位置を算出します。
 * @param {number} latitude 緯度です(単位は度数法)。
 * @param {number} longitude 経度です(単位は度数法)。
 * @param {number} radius 半径です。
 * @returns {THREE.Vector3} 3Dの座標です。
 */
const translateGeoCoords = (latitude, longitude, radius) => {
  // 仰角
  const phi = latitude * Math.PI / 180;
  // 方位角
  const theta = (longitude - 180) * Math.PI / 180;

  const x = -1 * radius * Math.cos(phi) * Math.cos(theta);
  const y = radius * Math.sin(phi);
  const z = radius * Math.cos(phi) * Math.sin(theta);

  return new THREE.Vector3(x, y, z);
};

translateGeoCoords()関数を使って緯度経度から地球上の位置を導き出す事ができるようになりました。

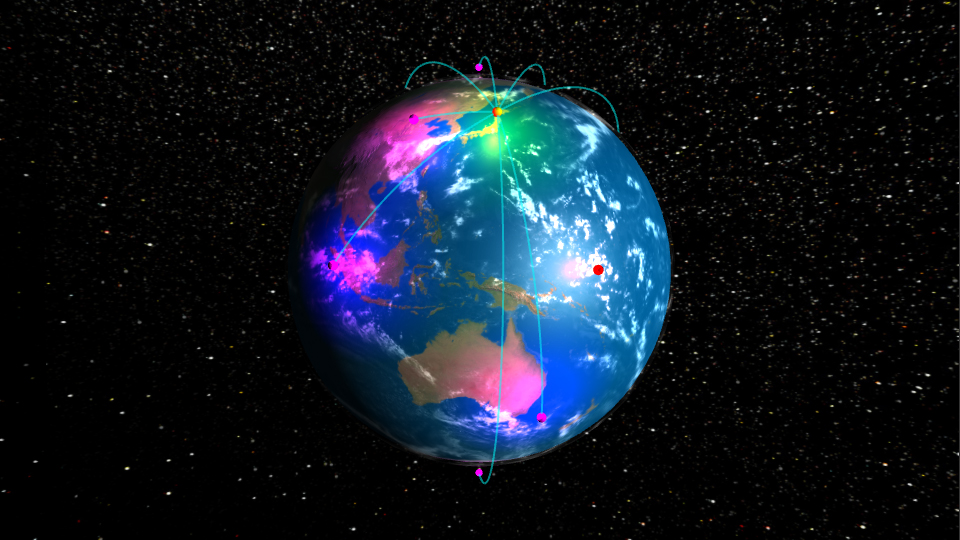
3. 球体状の2点を線でつなぐ

球体状の2点を線でつないでみましょう。次のサンプルでは、日本から世界の各都市へ線をつないでいます。航空会社のエアラインを示したかのような表現ができます。

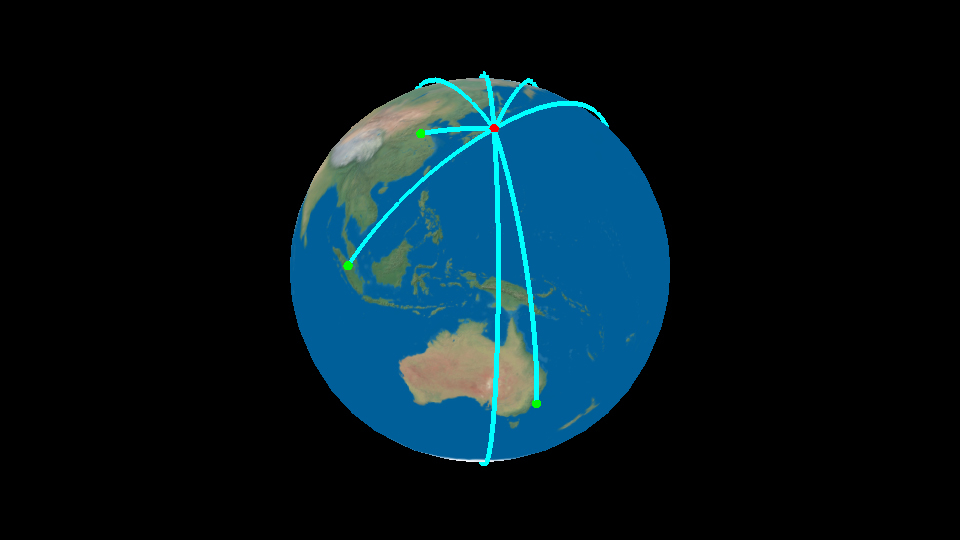
前章でプロットした地球上の点と点をつなぐ線を描いてみます。下図のような球状の2点間の軌跡座標を取得するには、クォータニオンを使用します。クォータニオンとは、回転軸と回転角度の情報を持っており、3D上でのオブジェクトの姿勢を表すものです。物体の回転を実装する上で役立ちます。

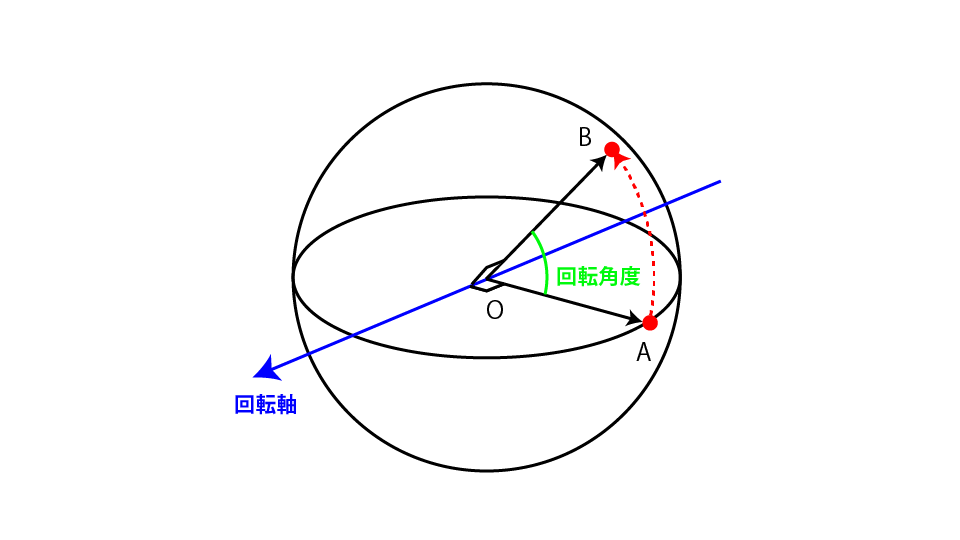
クォータニオンの詳しい説明は以下のサイトでわかりやすく解説されているのでこちらを参照ください。

先ほどの図を参考に、OAベクトルをOBベクトルに向かって少しずつ回転させ、軌道座標を配列で返す関数をJavaScriptで表現してみます。

/**
 * 軌道の座標を配列で返します。
 * 
 * @param {THREE.Vector3} startPos 開始点です。
 * @param {THREE.Vector3} endPos 終了点です。
 * @param {number} segmentNum セグメント分割数です。
 * @returns {THREE.Vector3[]} 軌跡座標の配列です。
 */
const createOrbitPoints = (startPos, endPos, segmentNum) => {
  // 頂点を格納する配列
  const vertices = [];
  const startVec = startPos.clone();
  const endVec = endPos.clone();

  // ２つのベクトルの回転軸
  const axis = startVec.clone().cross(endVec);
  // 軸ベクトルを単位ベクトルに
  axis.normalize();
  // ２つのベクトルが織りなす角度
  const angle = startVec.angleTo(endVec);

  // ２つの点を結ぶ弧を描くための頂点を打つ
  for (let i = 0; i < segmentNum; i++) {
    // axisを軸としたクォータニオンを生成
    const q = new THREE.Quaternion();
    q.setFromAxisAngle(axis, angle / segmentNum * i);
    // ベクトルを回転させる
    const vertex = startVec.clone().applyQuaternion(q);
    vertices.push(vertex);
  }

  // 終了点を追加
  vertices.push(endVec);
  return vertices;
};

クォータニオンを生成する上で必要な軸を作成します。今回の軸は、地球の中心から伸びた2つのベクトルのなす面に垂直なベクトルです。この場合、2つのベクトルの外積を求めることで垂直なベクトルを取得できるので、cross()メソッドを使用して軸となるベクトルを生成しましょう。

// 2つのベクトルの回転軸
const axis = startVec.clone().cross(endVec);

// 軸ベクトルを単位ベクトルに
axis.normalize();

先ほど作成した軸を基準にどこまで回転させるかを求めます。今回は、地球の中心から伸びた2つのベクトルのなす角度が回転角度の限界値になるのでangleTo()メソッドを用いて角度を求めます。

// 2つのベクトルのなす角度
const angle = startVec.angleTo(endVec);

回転軸と回転角度を求められたので、次にクォータニオンを生成します。なめらかな線を引くため、頂点の数分だけ少しずつ角度をつけていきます。

// axisを軸としたクォータニオンを生成  
const q = new THREE.Quaternion();

// setFromAxisAngle(回転軸, 回転角度)  
q.setFromAxisAngle(axis, angle / segmentNum * i);

クォータニオンで作った回転情報をOAベクトルに反映させます。

// ベクトルを回転させる
const vertex = startVec.clone().applyQuaternion(q);

二点を結ぶ軌跡の座標をcreateOrbitPoints()関数から算出できるようになりました。軌跡座標を線の頂点として設定することで、デモのように二点間を結ぶ軌跡を表現できます。

まとめ

円形・球体の座標制御に三角関数が役立つことがわかっていただけたのではないでしょうか。一般的に3Dのサンプルに地球や天体を使用したものが多いですが、これらの数式・概念がわかっているとサンプルコードが読み解きやすくなります。冒頭のデモは3つのサンプルから少しだけ装飾を付け加えたものなので、応用編として挑戦してみてください。

今回はThree.jsを使用して三角関数によるグラフィックを作成しましたが、この数式と概念は他の言語やライブラリでも同じように活用できます。2次元での三角関数の活用方法も記事「CreateJS入門」や「CSSの三角関数を理解しよう！ sin()とcos()でできる表現」で解説しています。ぜひ、三角関数を使った表現を試してみてください。

※この記事が公開されたのは8年前ですが、1年前の2023年3月に内容をメンテナンスしています。

ICS MEDIA